Art of Multiprocessor Programming Summary

in Dev. Log on Concurrent Programming

GitHub issue author

This is short(?) summary of the textbook “Art of Multiprocessor Programming” by Maurice Herlihy & Nir Shavit.
A complete set of lecture slides & sample code is available at the textbook’s companion page
This work is licensed under a Attribution-ShareAlike 3.0.

Introduction

Asynchronous Computation

  • Safety Properties: Nothing bad happens ever
    • Mutual Exclusion
  • Liveness Properties: Something good happens eventually
    • No Deadlock

“Alice & Bob share a pond” / Mutual Exclusion

  • Cell Phone Protocol
    • One calls the other.
    • Problem: recipient might not be listening or not there at all.
      Communication must be persistent / not transient
  • Flag Protocol
    Raise flag -> wait until other’s flag is down -> unleash pet -> lower flag after return
    • What if both raises flag?? : Deadlock Raise flag -> while other’s flag is up, lower flag & wait -> raise flag -> …
    • One must always defer for other. (Unfair & waiting)

Mutual Exclusion

  • cannot be solved by transient communication / interrupts
  • can be solved by one-bit shared variable

Producer - Consumer

  1. Producer must inform Consumer when product is ready.
  2. Consumer must inform Producer if there is no product to use.

Solution

  • Producer owns a can.
    • knocks over can when product is ready.
    • reset can when product is all used up.

  • Consumer

    while (true) {
  while (can.isUp()) {};
  pet.release();
  pet.recapture();
  can.reset();
}

  • Producer

    while (true) {
  while (can.isDown()) {};
  pond.stockWithFood();
  can.knockOver();
}
  • Correctness
    • Mutual Exclusion -> safety
      pet & Bob never together in pond
    • No Starvation -> liveness
    • Producer/Consumer -> safety
      The pet never enter pond unless there is food / Bob never provide food if there is unconsumed food.

Amdahl’s Law

speed up = single thread execution time / n-thread execution time

let p = parallel fraction, n = number of threads

speed up = 1 / (1 - p + p/n)

Mutual Exclusion

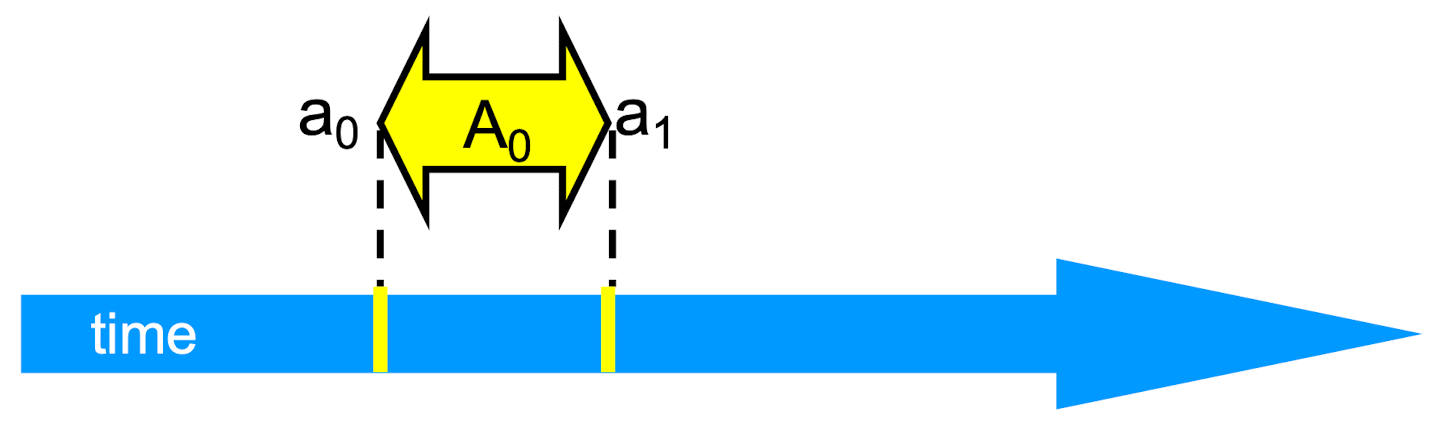
An event a0 of thread A is

  • Instantaneous
  • No simultaneous events (break ties)

Interval

An interval A0 = (a0, a1) is Time between events a0 and a1

interval

Precedence

precedence

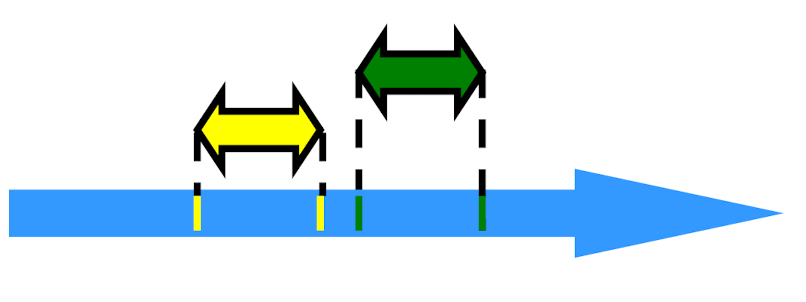
  • Notation: A0 -> B0

  • End event of A0 before start event of B0
  • Precedence Ordering
    • Irreflexive: Never true that A -> A
    • Antisymmetric: If A - > B then not true that B -> A
    • Transitive: If A -> B & B -> C then A -> C
    • A -> B & B -> A might both be false! (Overlap)

Deadlock-Free

System as a whole makes progress

  • even if individuals starve

Starvation-Free

Individual threads make progress

Lock

Peterson’s Algorithm (2 threads)

public void lock() {
 flag[i] = true;
  victim = i;
  while (flag[j] && victim == i) {}; //spin-wait
}

public void unlock() {
  flag[i] = false;
}
  • Solo: other’s flag is false
  • Both: one or the other not the victim
  • Starvation-Free

Filter Algorithm (n threads)

class Filter implements Lock {
  int[] level;  // level[i] for thread i
  int[] victim; // victim[L] for level L

  public Filter(int n) {
    level  = new int[n];
    victim = new int[n];
    for (int i = 1; i < n; i++) {
      level[i] = 0;
    }
  }

  public void lock() {
    for (int L = 0; L < n; L++) {
      level[i] = L;
      victim[L] = i;
      while(((∃k != i) level[k] >= L)) && victim[L] == i) {};
      // thread enters level L when it completes the loop above.
    }
  }

  public void unlock(int i) {
    level[i] = 0;
  }
}

There are n-1 levels.

  • At each level
    • At least one enters level
    • At least one blocked if many try
  • Only one thread makes it through
  • At most n-L threads enter level L
  • mutual exclusion at level L = n-1
  • Starvation-Free but weak fairness(overtaken by others who come lately)

Bakery Algorithm

class Bakery implements Lock {
  boolean[] flag;
  Label[] label;

  public Bakery(int n) {
    flag  = new boolean[n];
    label = new Label[n];
    for (int i = 0; i < n; i++) {
      flag[i]  = false;
      label[i] = 0;
    }
  }

  public void lock() {
    flag[i]  = true;
    label[i] = max(label[0], ..., label[n-1]) + 1;
    while (∃k flag[k] && label[i] > label[k]) {};
    // acquire lock iff my label is lowest
  }

  public void unlock() {
    flag[i] = false;
  }
}
  • Provides FCFS
    • Take a number
    • Wait until lower numbers have been served
    • good fairness
  • No deadlock

Concurrent Object

Sequential Specifications for Method

  • Each method described in isolation

  • Precondition: if
    • the object’s state before call the method
  • Postcondition: then
    • return value or exception
    • the object’s state after method return

Example - dequeue

  • Precondition: Queue is non-empty
  • Postcondition: Returns first item in queue / Removes first item in queue Precondition: Queue is empty

Postcondition: Throws empty exception / Queue state unchanged

Concurrent Specifications

  • Method call is not an event

  • Method call is an interval
    • Must characterize all possible interactions with concurrent calls.

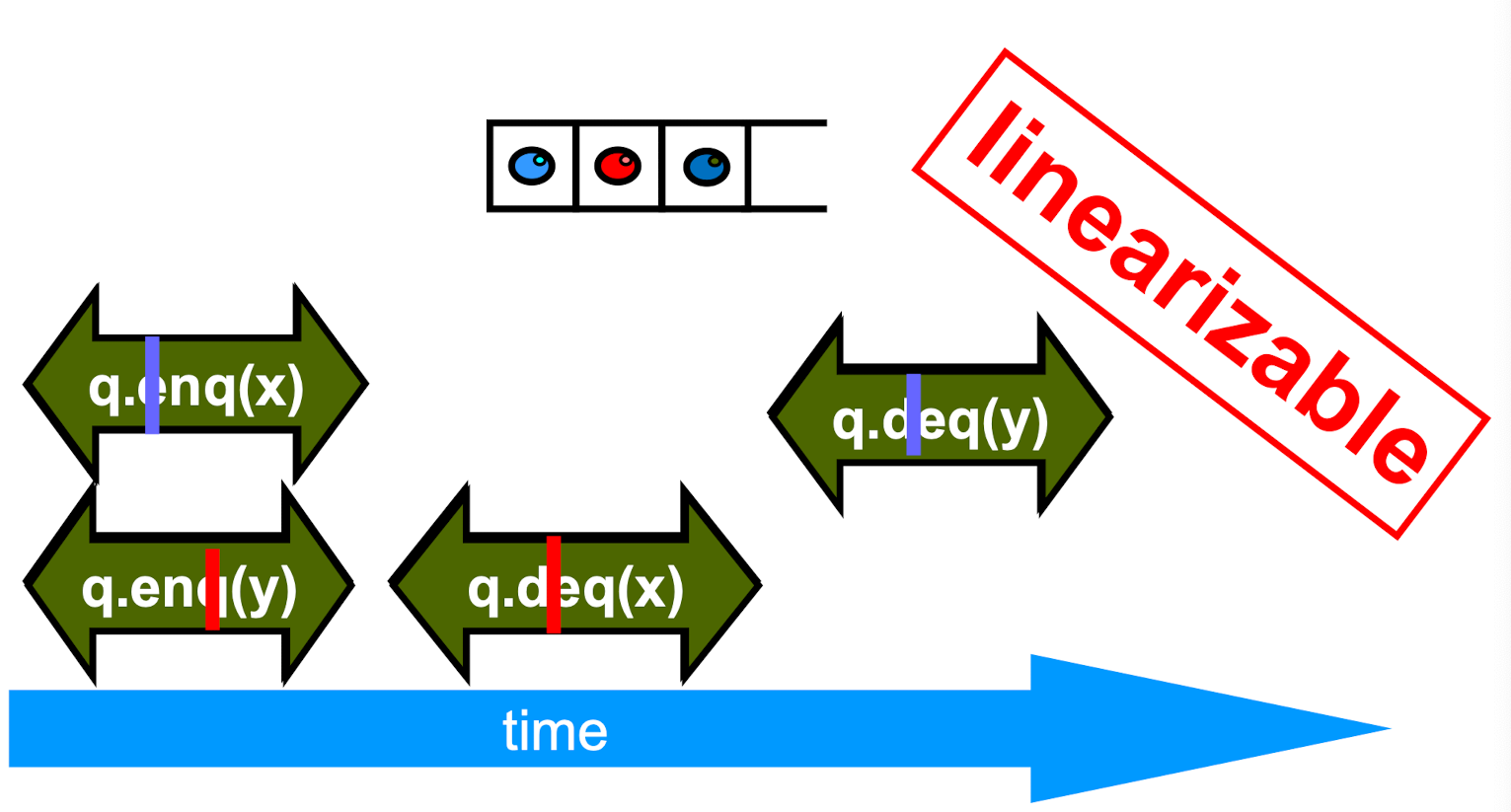
  • Linearizable Object

    • One all of whose possible executions are linearizable

    linearizable object

Notations

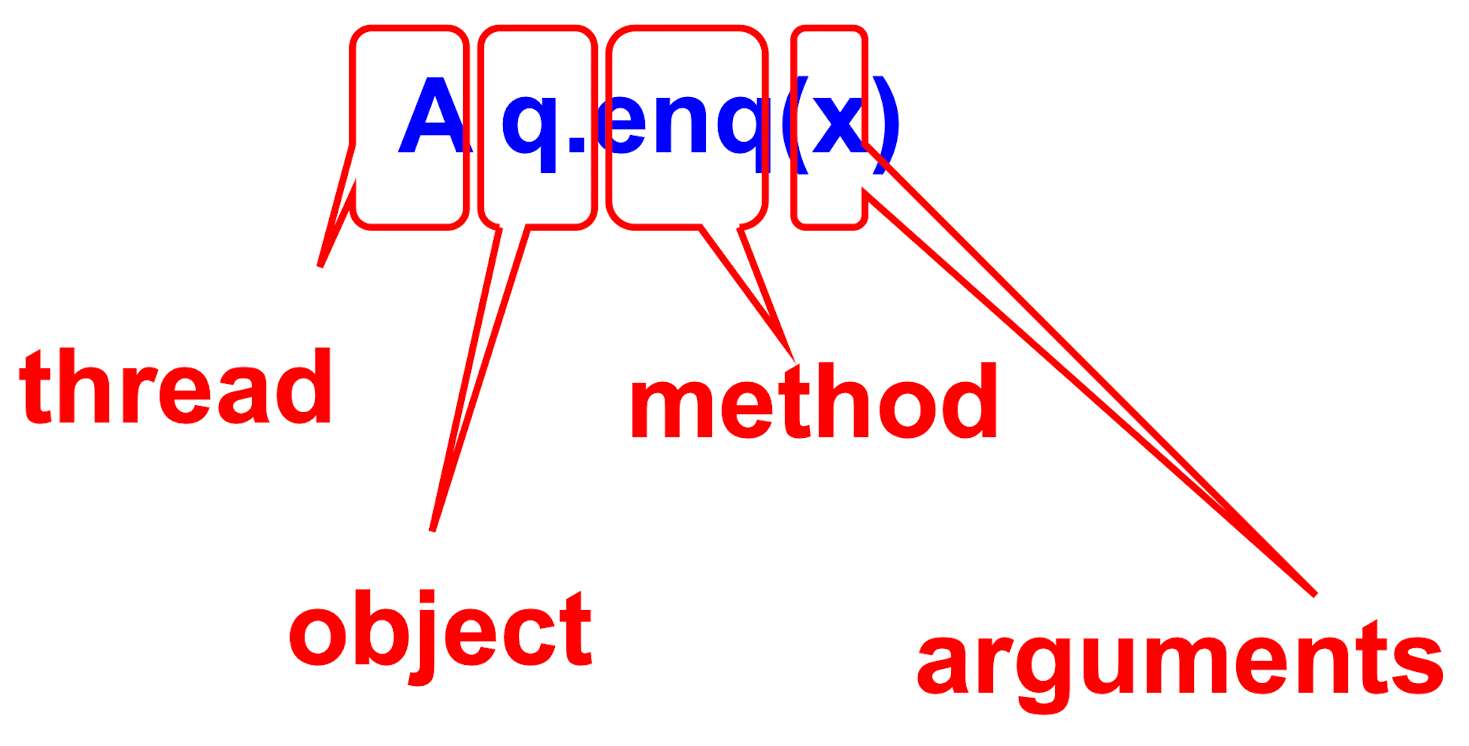
Invocation Notations

invocation notation

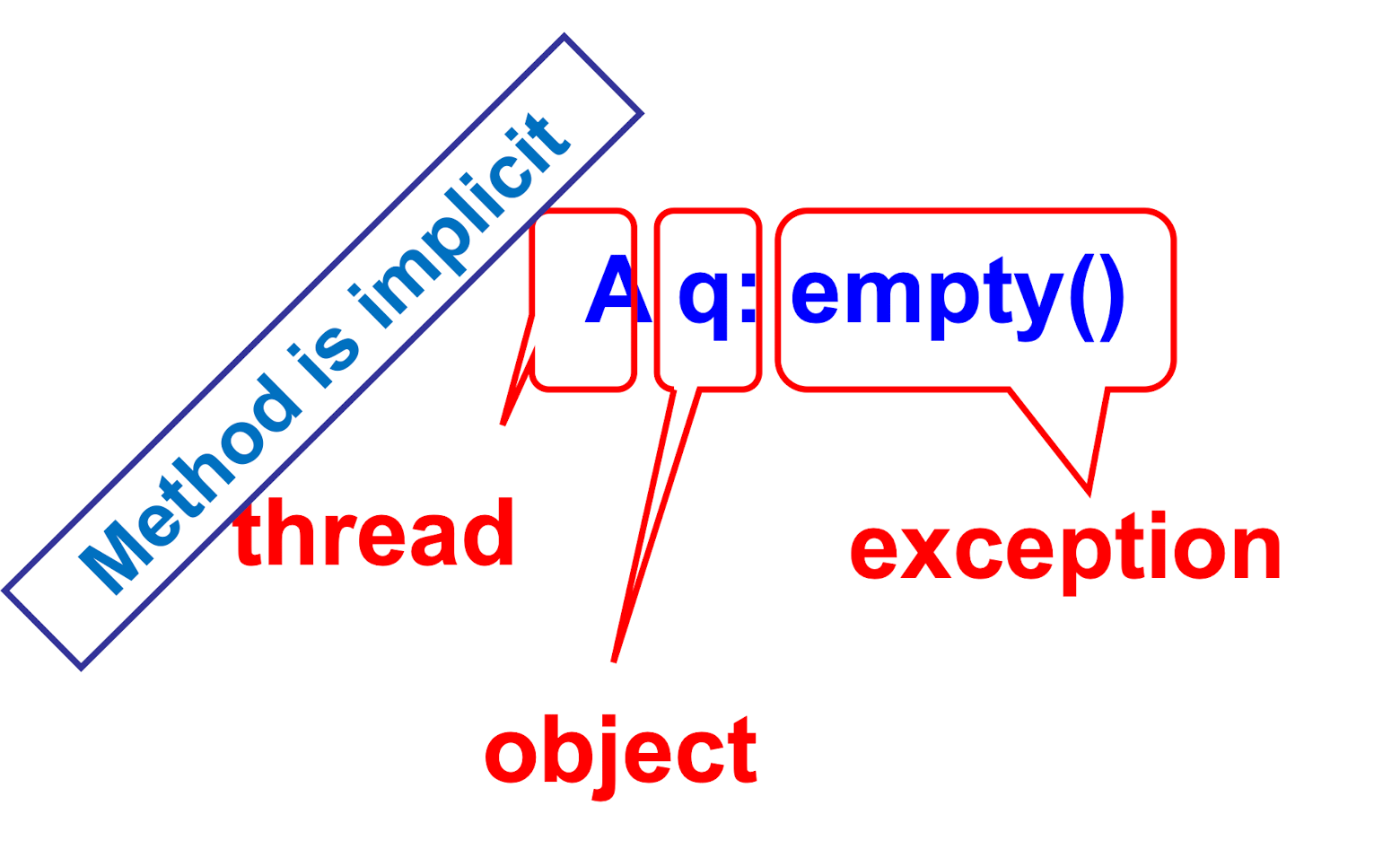
Response Notation

response notation

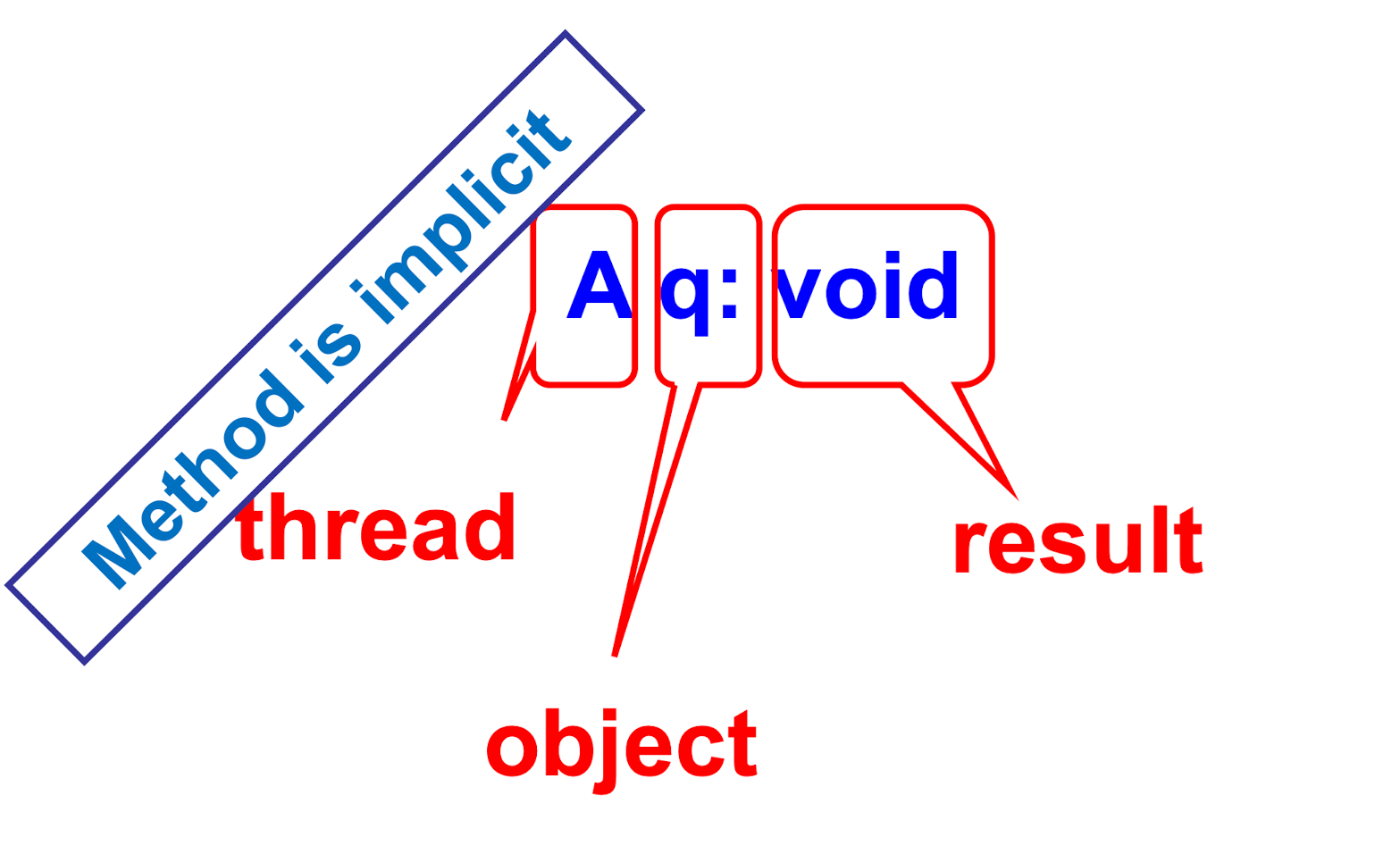
exception notation

History

  • Describing an Execution

history

  • Invocation & Response match if
    • thread names agree & object names agree
  • Invocation is pending if
    • it has no matching response
    • may or may not have taken effect
  • Object Projections
    object projections
  • Thread Projections
    thread projections

Complete Subhistory

  • discard pending invocation

Sequential Histories

sequential histories

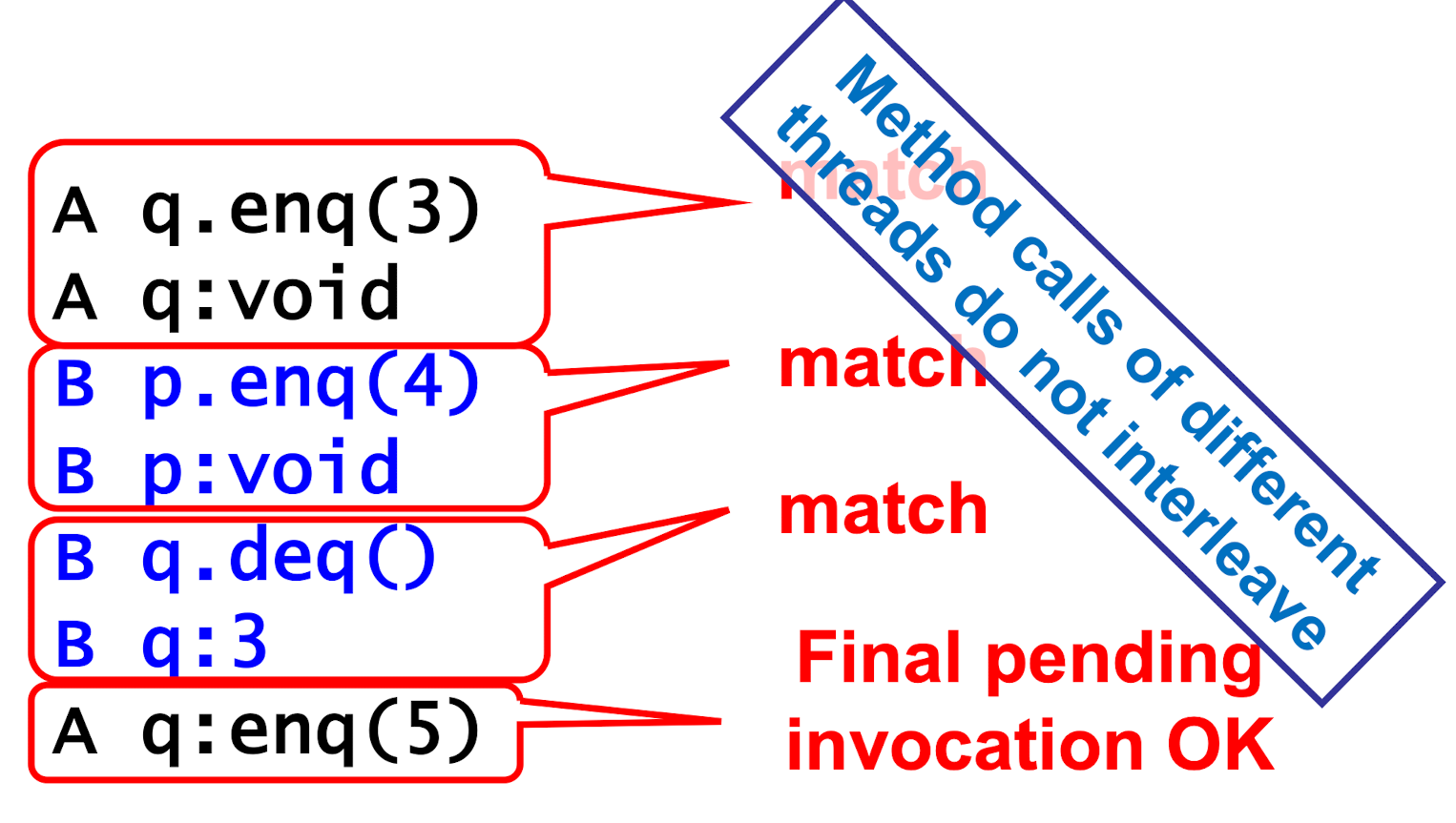
Well-Formed Histories

  • Per-thread projections are sequential

Equivalent Histories

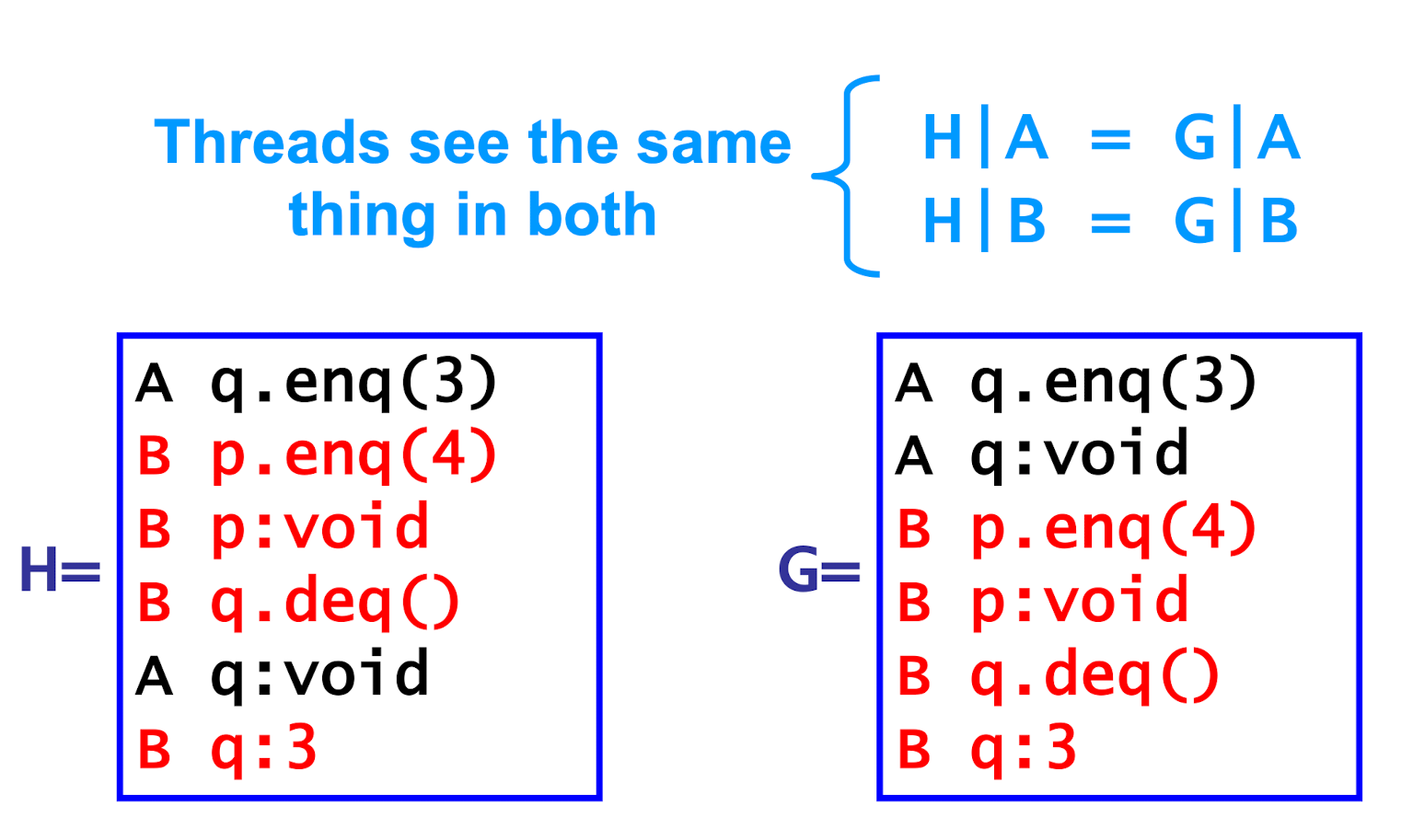
equivalent histories

  • For every object x, **Hx** is in the sequential spec for x

Precedence

  • A method call precedes another if response event precedes invocation event

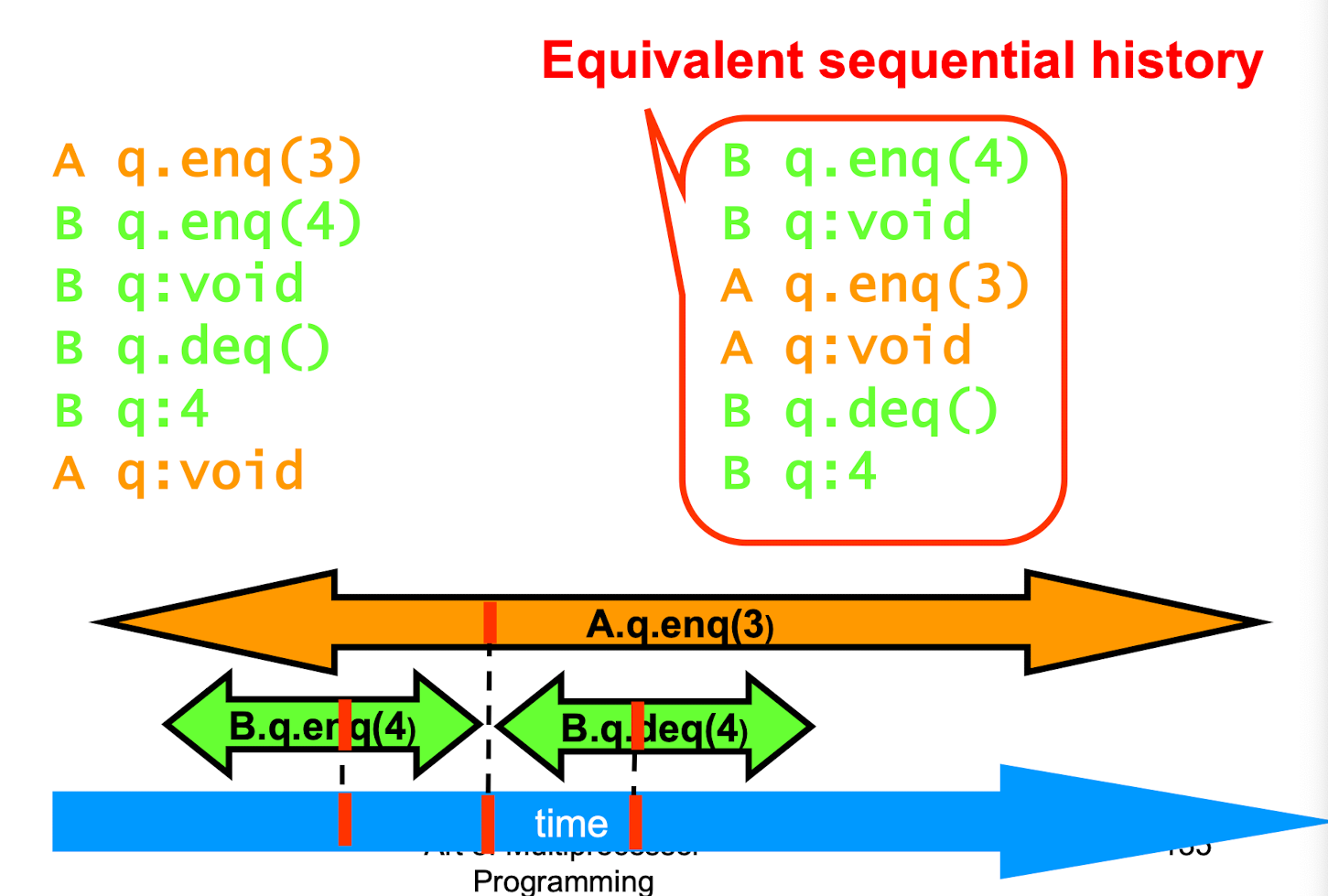
Linearizability

  • History H is linearizable if it can be extended to G by
    • Appending zero or more responses to pending invocations
    • Discarding other pending invocations
  • So that G is equivalent to
    • Legal sequential history S
    • Where ->G ⊂ ->S
    • Means that S respects “real-time order” of G

    legal sequential history

Composability Theorem

  • History H is linearizable iff
    • For every object x
    • *Hx* is linearizable

Foundations of Shared Memory

Turing Computability

  • Mathematical model of computation
  • What is (and is not) computable

Shared-Memory Computability

  • Mathematical mode of concurrent computation
  • What is (and is not) concurrently computable
  • Efficiency (mostly) irrelevant

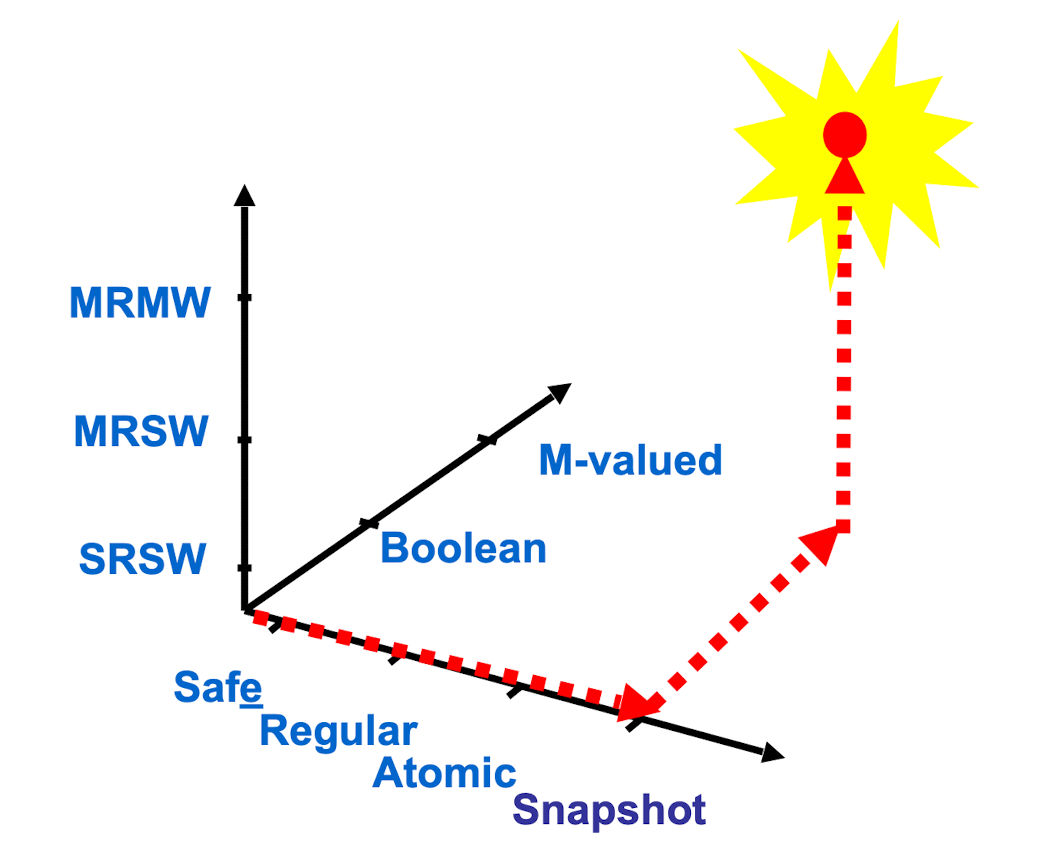
Wait-Free

  • every method call completes in a finite # of steps

Safe Register

  • OK if reads & writes don’t overlap
  • Some valid value if reads & writes do overlap

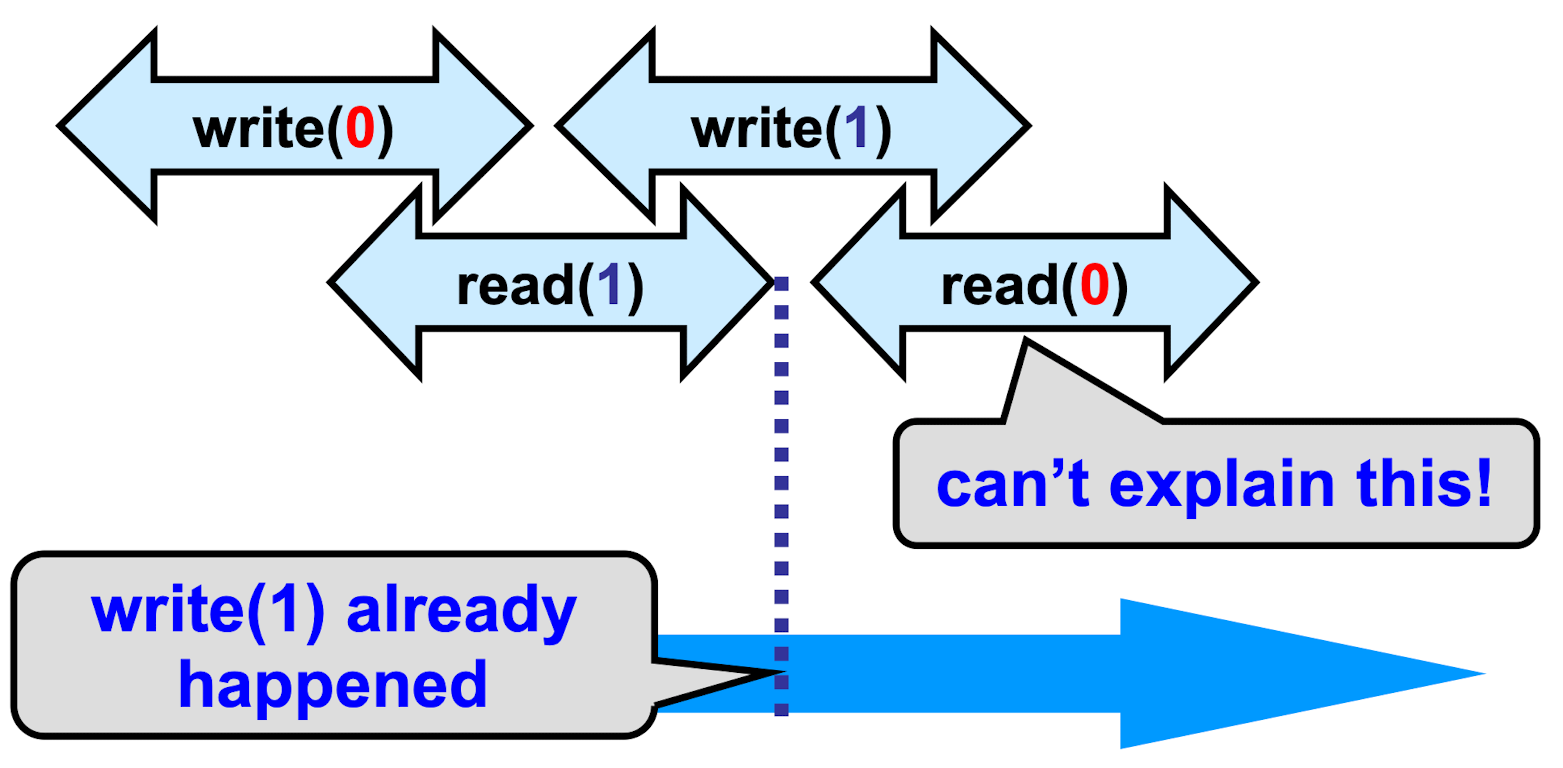
Regular Register

  • old or new value if overlap

  • Regular ≠ Linearizable

    regular is not linearizable

Road Map

safe to atomic snapshot

SRSW Safe Boolean

  • Get correct reading if not during state transition

MRSW Safe Boolean

public class SafeBoolMRSWRegister implements Register<Boolean> {
  private SafeBoolSRSWRegister r = new SafeBoolSRSWRegister[N];

  public void write(boolean x) {
    for (int j = 0; j < N; j++)
      r[j].write(x);
  }

  public boolean read() {
    int i = ThreadID.get();
    return r[i].read();
  }
}
  • Multi-Valued MRSW also works

MRSW Regular Boolean

  • Naive Approach : problem occurs if writer writes same value.
    • Don’t perform write if old value is equal to input
public class RegBoolMRSWRegister implements Register<Boolean> {
  private boolean old;
  private SafeBoolMRSWRegister value;

  public void write(boolean x) {
    if (old != x) {
      value.write(x);
      old = x;
    }
  }

  public boolean read() {
    return value.read();
  }
}

MRSW Regular

  • Multi-Valued register
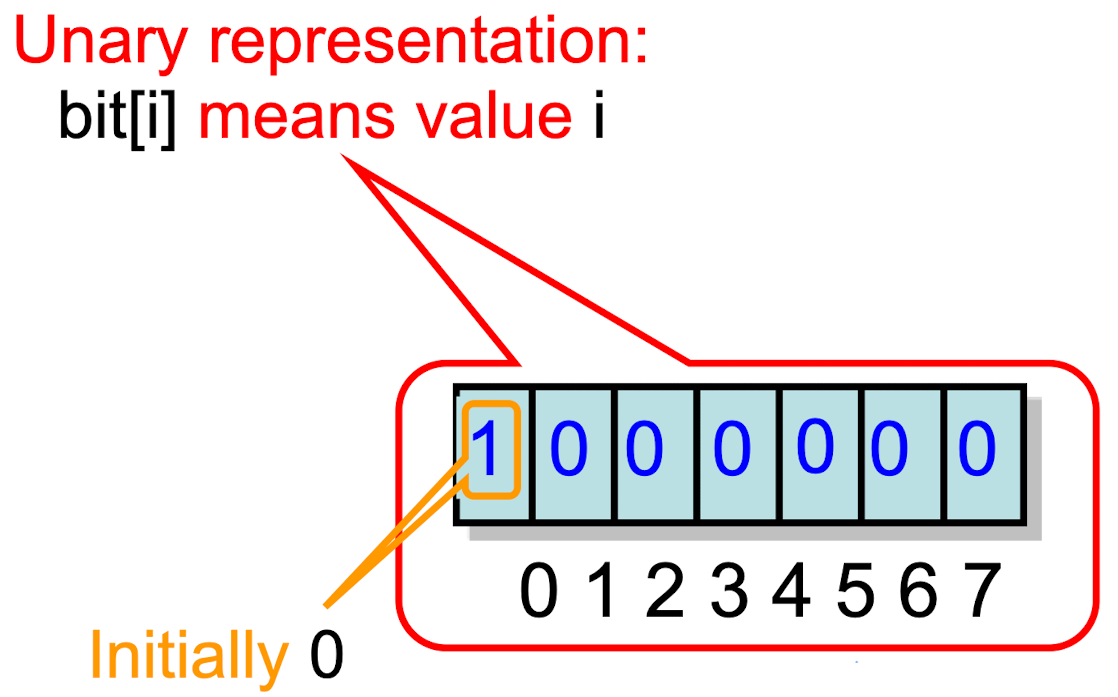
    multi-value
public class RegMRSWRegister implements Register {
  RegBoolMRSWRegister[M] bit;
  public void write(int x) {
    this.bit[x].write(true);
    for (int i = x-1; i >= 0; i--) {
      this.bit[i].write(false);
    }
  }

  public int read() {
  for (int i = 0; i < M; i++) {
      if (this.bit[i].read())
        return i;
    }
  }
}

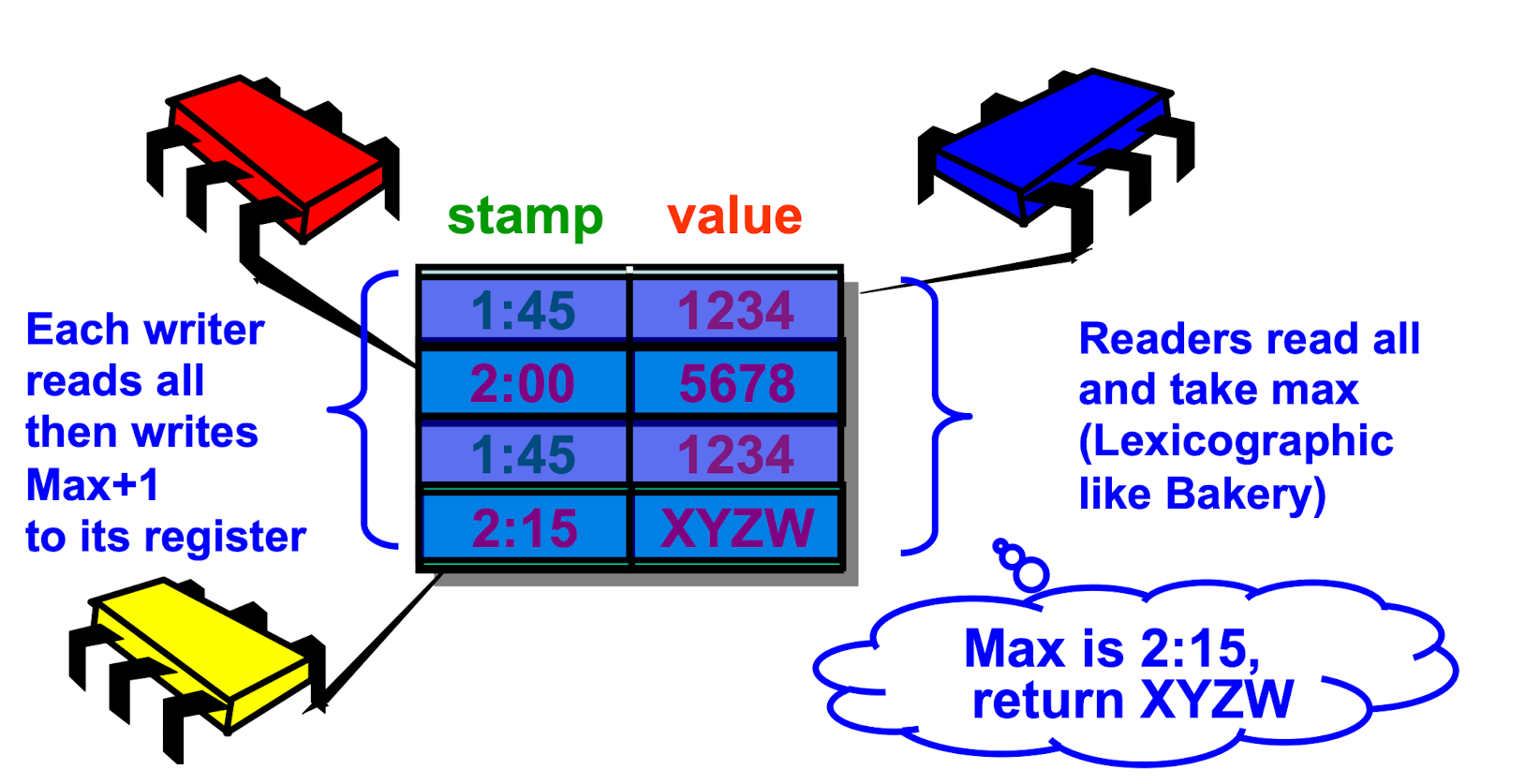
SRSW Atomic

  • Timestamped Values
    • Writer writes value & stamp together
    • Reader saves last value & stamp read
    • Reader returns new value iff stamp is higher

MRSW Atomic

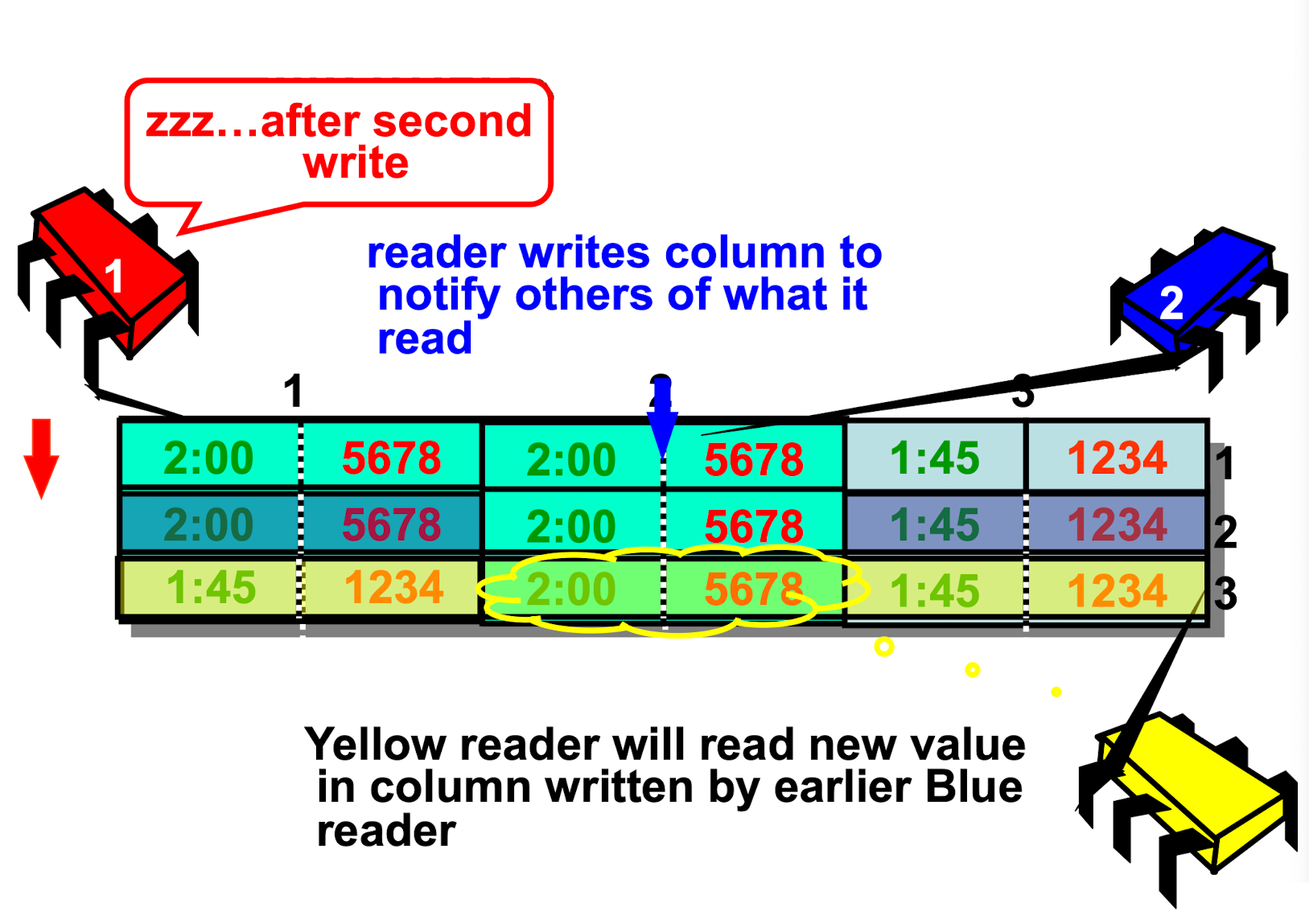
mrsw atomic

  • Yellow may miss Blue’s update iff they overlap.

MRMW Atomic

mrmw atomic

Atomic Simple Snapshot

  • Array of MRSW atomic registers
  • Collect twice
    • If both agree, done
    • otherwise, redo
public class SimpleSnapshot implements Snapshot {
  private AtomicMRSWRegister[] register;

  public void update(int value) {
    int i = Thread.getID();
    LabeledValue oldValue = register[i].read();
    LabeledValue newValue = new LabeledValue(oldValue.label+1, value);
    register[i].write(newValue);
  }

  private LabeledValue[] collect() {
    LabeledValue[] = copy = new LabeledValue[n];
    for (int i = 0; i < n; i++)
      copy[i] = this.register[j].read();
    return copy;
  }

  public int[] scan() {
    LabeledValue[] oldCopy, newCopy;
    oldCopy = collect();
    redo:
    while (true) {
      newCopy = collect();
      if (!equals(oldCopy, newCopy)) {
        oldCopy = newCopy;
        continue redo;
      }
      return getValues(newCopy);
    }
  }
}
  • Linearizable
  • update() is wait-free
  • scan() can starve

Wait-Free Snapshot

  • Add a scan() before update()
  • If scan() is continuously interrupted by updates, scan() can take the update’s snapshot

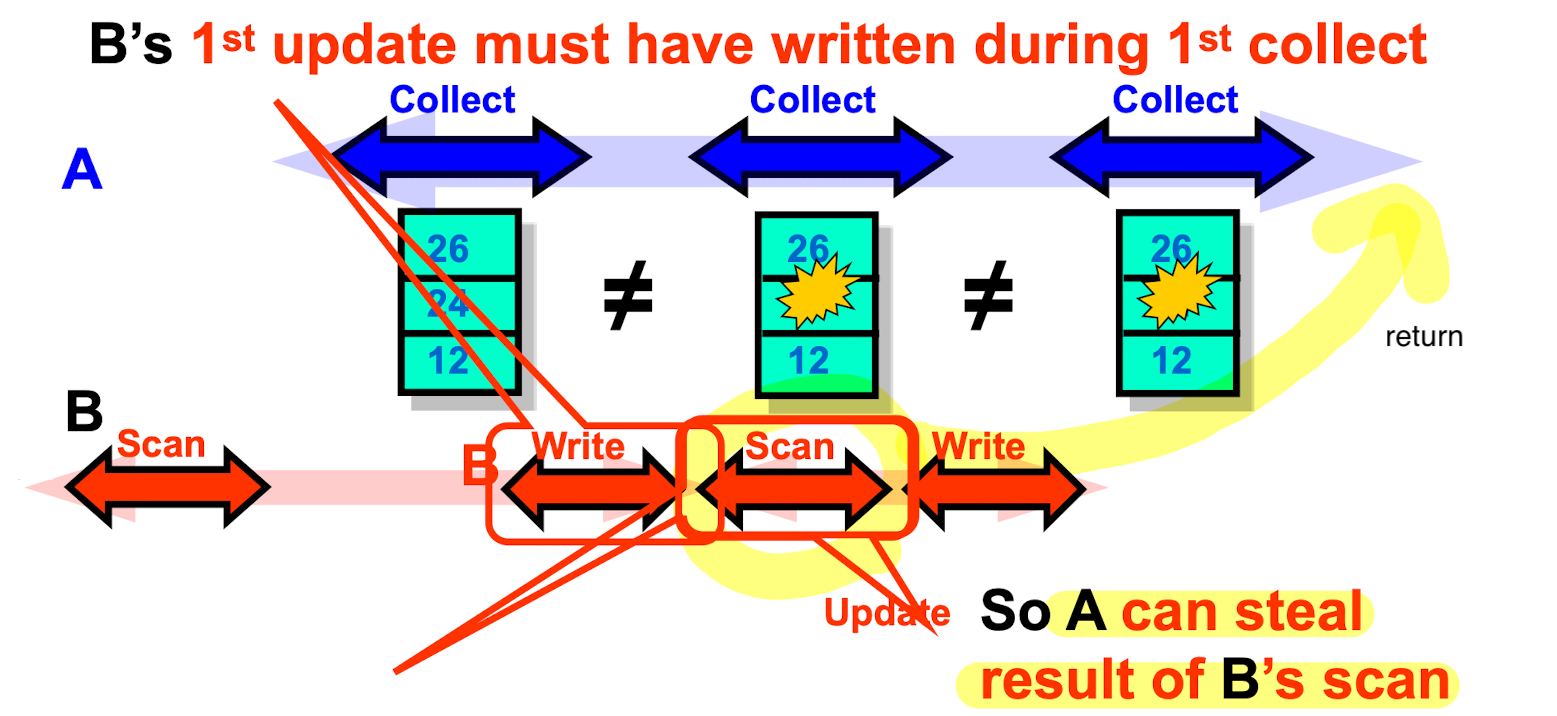
wait-free snapshot

  • If same thread interrupts twice, take it’s snapshot.
  • scan() can only be interrupted at most n-1 times before taking update’s snapshot(thus wait-free)
public class SnapValue {
 public int   label;
 public int   value;
  public int[] snap;  // most recent snapshot taken by update
}

public class WaitFreeSnapshot implements Snapshot {
  private AtomicMRSWRegister[] register;

  public void update(int value) {
    int i = Thread.getID();
    int[] snap = this.scan(); // scan before write
    SnapValue oldValue = r[i].read();
    SnapValue newValue = new SnapValue(oldValue.label+1, value, snap);
    r[i].write(newValue);
  }

  private SnapValue[] collect() {
    SnapValue[] = copy = new SnapValue[n];
    for (int i = 0; i < n; i++)
      copy[i] = this.register[j].read();
    return copy;
  }

  public int[] scan() {
    SnapValue[] oldCopy, newCopy;
    boolean[] moved new boolean[n];
    oldCopy = collect();
    redo:
    while (true) {
      newCopy = collect();
      for (int i = 0; i < n; i++) {
        if (oldCopy[i].label != newCopy[i].label) {
          if (moved[i]) { // second move
            return newCopy[i].snap;
          } else {
            moved[i] = true;
            oldCopy = newCopy;
            continue redo;
          }
        }
      }
      return getValues(newCopy);
    }
  }
}

The Relative Power of Synchronization Operations

Wait-Free Implementation

  • Every method call completes in finite number of steps
  • Implies no mutual exclusion

Problem of Mutual Exclusion

  • Asynchronous Interrupts
    • owner swapped out
  • Heterogeneous Processors
    • owner is very slow processor
  • Fault-tolerance
    • owner is crashed
  • Machine Level Instruction Granularity
    • Amdahl’s Law

Consensus

  • Consistent
    • All threads decide the same value
  • Valid
    • The common decision value is some thread’s input

Wait-Free Computation

wait-free computation

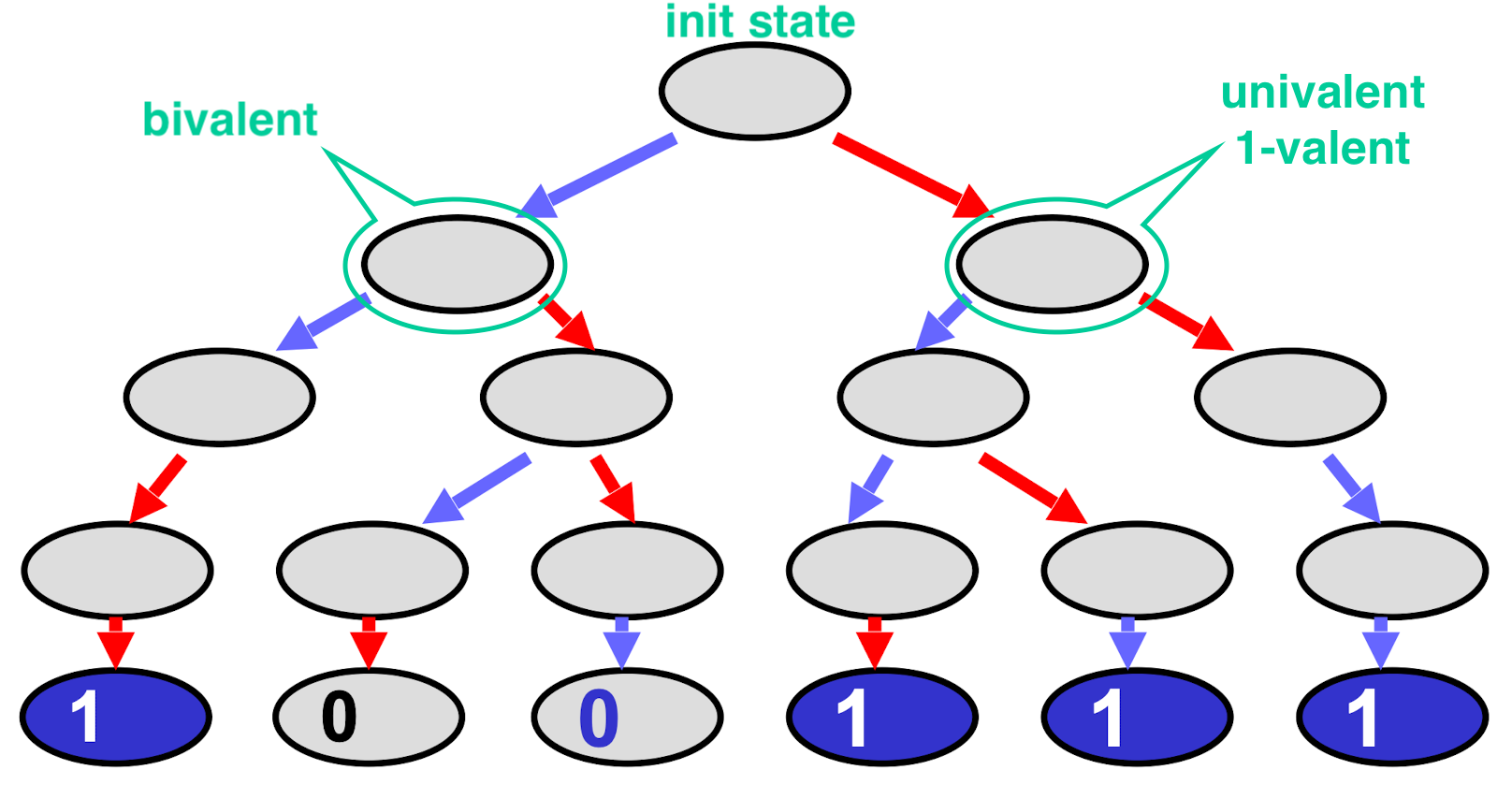
  • Wait-free computation is a tree
  • Bivalent State means outcome is not fixed

  • Univalent State means outcome is fixed

  • 0-Valent & 1-Valent state means outcome is fixed to n
  • Some initial state is bivalent
  • Outcome depends on
    • chance
    • who runs by scheduler
  • Critical State
    • If A goes first, protocol decides 0
    • If B goes first, protocol decides 1
    • Protocol can reach a critical state
      • Otherwise it will stay bivalent forever thus not wait-free

Atomic Registers Can’t Do Consensus

  • If protocol exists
    • It has a bivalent initial state leading to a critical state.
  • But all possible pair of methods(read & write) lead to a contradiction.

FIFO Queue Implementation of Consensus

Generic Consensus Protocol

abstract class ConsensusProtocol<T> implements Consensus<T> {
  protected T[] proposed = new T[N];

  protected void propose(T value) {
    proposed[Thread.getID()] = value;
  }

  abstract public T decide(T value);
}
Queue Consensus
public class QueueConsensus<T> extends ConsensusProtocol<T> {
  private Queue queue;

  public QueueConsensus() {
   queue = new Queue();
    queue.enq(Ball.RED);   // Thread that dequeues RED ball will decide value
    queue.enq(Ball.BLACK); // Thread with BLACK ball will use RED ball owner's proposed value.
  }

  public T decide(T value) {
    propose(value);
    Ball ball = queue.deq();
    if (ball == Ball.RED)
      return proposed[i];   // I got the red. Use my proposed value
    else
      return proposed[1-i]; // I got black ball. Use other's proposed value.
  }
}
  • We can solve 2-thread consensus using only a two-dequeuer queue
  • Problem
    • It is impossible to implement a two-dequeuer wait-free FIFO queue with read/write memory

Consensus Numbers

  • An object X has consensus number n
    • If it can be used to solve n-thread consensus together with atomic read/write registers
  • Theorem
    • If you can implement X from Y. And X has consensus number n, then Y has consensus number at least n
    • Conversely, if X has consensus number n. And Y has consensus number m < n, then there is no way to construct a wait-free implementation of X by Y
    • Example : Multiple Assignment Theorem
      • Atomic registers cannot implement multiple assignment
      • If we can write to 2 slots out of 3 array locations, we can solve 2-consensus -> which is impossible with atomic registers(consensus number 1)
      • Therefore cannot implement multiple assignment with atomic registers

Read-Modify-Write Objects

  • Method call returns object’s prior value x, replace value x with func(x)

    public int synchronized RMWmethod() {
  int prior = value;
  value = func(value);
  return prior;
}
  • A RMW method is non-trivial if
    • there exists a value v such that v ≠ func(v)
  • Any non-trivial RMW object has consensus number at least 2
    • Meaning, no wait-free implementation of RMW registers from atomic registers
    // A two-thread consensus protocol using any non-trivial RMW object
public class RMWConsensus extends ConsensusProtocol {
  private RMWRegister r = v;

  public decide(T value) {
    int i = Thread.getID();
    propose(value);
    if (r.getAndMumble() == v) // I'm the first
      return proposed[i];
    else
      return proposed[1-i];
  }
}
  • Any set of RMW objects that commutes or overwrites has consensus number exactly 2
    • Commute: fi(fk(v))) = fk(fi(v)))
    • Overwrite: fi(fk(v))) = fi(v)
    • test-and-set, swap(getAndSet), fetch-and-inc
    • Can be proved by using critical section analysis with three threads.

  • compare-and-set has ∞ consensus number

    public class RMWConsensus extends ConsensusProtocol {
  private AtomicInteger r = new AtomicInteger(-1);

  public T decide(T value) {
  int i = Thread.getID();
    propose(value);
    r.compareAndSet(-1, i);  // Winner(who runs CAS first) will set r value to it's ID.
    return proposed[r.get()];
  }
}

Lock-Free vs. Wait-Free

  • Wait-Free: each method call takes a finite number of steps to finish
  • Lock-Free: infinitely often some method call finishes
    • Any wait-free implementation is lock-free

Universality of Consensus

Universality

  • Consensus is universal
  • From n-thread consensus we can build a
    • Wait-Free
    • Linearizable
    • n-threaded implementation
    • Of any sequentially specified object

Lock-Free Universal Construction

Naive Idea

  • Consensus object stores reference to cell with current state
  • Each thread creates new cell
    • contains next state after computation
    • tries to switch pointer to its outcome
  • Fail!
    • Consensus objects can be used only once

Linked-List Representation

  • Shows global execution order in LL foam

  • Each node contains a pointer to fresh consensus object used to decide on next operation

  • Object represented as

    • Initial Object state
    • A Log: a linked list of the method calls
Lock-Free Construction
public class Node {
  public Invoc invoc;
  public Consensus<Node> decideNext;
  public Node next;
  public int seq;

  public Node(Invoc invoc) {
    invoc = invoc;
    decideNext = new Consensus<Node>();
    seq = 0;
  }
}

public class Universal {
  private Node[] head;
  private Node tail;

  public Universal() {
    head = new Node[N];
    tail = new Node();
    tail.seq = 1;
    for (int i = 0; i < n; i++)
      head[i] = tail;
  }

  public static Node max(Node[] arr) {
    Node maxi = arr[0];
    for (int i = 1; i < arr.length; i++)
      if (maxi.seq < arr[i].seq)
        max = arr[i];
    return maxi;
  }

  public Response apply(Invoc invoc) {
    int i = Thread.getID();
    Node prefer = new node(invoc);
    while (prefer.seq == 0) {
      // repeat until my prefer got selected by decide().
      Node before = Node.max(head);
      Node after = before.decideNext.decide(prefer);
      before.next = after;
      after.seq = before.seq + 1;
      head[i] = after;
    }
    // sequentially apply all previous & my invoc.
    seqObject obj = new SeqObject();
    Node curr = tail.next;
    while (curr != prefer) {
      obj.apply(curr.invoc);
      curr = curr.next;
    }
    return obj.apply(curr.invoc);
  }
}
  • Contention: All threads repeatedly modify head
    • Solution: Make head an array
      Thread i updates location i
      Find head by finding max seq of nodes referenced by head array
    • Still not wait-free

Wait-Free Construction

  • Lock-Free Construction + announce array
  • Stores pointer to node in announce
    • If a thread doesn’t append its node
    • Another thread will see it in announce array and help append it
public class Universal {
  private Node[] announce;
  private Node[] head;
  private Node tail;

  public Universal() {
    announce = new Node[N];
    head = new Node[N];
    tail = new Node();
    tail.seq = 1;
    for (int i = 0; i < n; i++) {
      announce[i] = tail;
     head[i] = tail;
    }
  }

  public Response apply(Invoc invoc) {
    int i = Thread.getID();
    announce[i] = new Node(invoc); // Announce new method call, asking help from others
    head[i] = Node.max(head);
  while (announce[i].seq = 0) {
      Node before = head[i];
      Node help = announce[(before.seq + 1) % n]; // Choose random announce for candidate
      if (help.seq == 0)
        prefer = help;
      else
        prefer = announce[i]; // If candidate is already inserted, mind own business
    }
  }
}

Spin Locks and Contention

Architectures

  • SISD (Uniprocessor)
    • Single instruction stream
    • Single data stream
  • SIMD (Vector)
    • Single instruction
    • Multiple data
  • MIMD (Multiprocessors)
    • Multiple instruction
    • Multiple data
      • Shared Bus
        • Cheap, but must wait for snooping (communication contention/latency)
        • If destination is same, one must be blocked (memory contention)
      • Distributed
        • All to all communication
        • Much more complicated circuit
        • Each core has own caches/bus

What Should You Do If You Can’t Get a Lock

  • Keep trying
    • “spin” or “busy-wait”
    • Good if delays are short
  • Give up the processor
    • Good if delays are long
    • Always good on uniprocessor

Test-and-Set Lock

public class AtomicBoolean {
  boolean value;

  public synchronized boolean getAndSet(boolean newValue) {
    boolean prior = value;
    value = newValue;
    return prior;
  }
}

AtomicBoolean lock = new AtomicBoolean(false);
...
boolean prior = lock.getAndSet(true);
  • Locking
    • Lock is free: value is false
    • Lock is taken: value is true
  • Acquire lock by calling TAS
    • If result is false, you win
    • If result is true, you lose
  • Release lock by writing false
class TASlock {
  AtomicBoolean state = new Atomicboolean(false);

  void lock() {
    while (state.getAndSet(true)) {};
  }

  void unlock() {
    state.set(false);
  }
}
  • Space complexity: O(1)
  • Performance: Bad, so many cache invalidation

Test-and-Test-and-Set Lock

  • Don’t call TAS if lock is acquired
    • Less cache invalidation
class TTASlock {
  AtomicBoolean state = new AtomicBoolean(false);

  void lock() {
    while (true) {
      while (state.get()) {}; // read-only: no cache invalidation
      if (!state.getAndSet(true))
        return;
    }
  }
}

Cache

Fully Associative Cache

  • Any line can be anywhere in the cache
    • Pros: can replace any line
    • Cons: hard to find lines (performance issue)

Direct Mapped Cache

  • Every address has exactly 1 slot
    • Pros: easy to find a line
    • Cons: must replace fixed line

K-way Set Associative Cache

  • Each slot holds k lines
    • Pros: pretty easy to find a line
    • Cons: some choice in replacing line

Cache Coherence Protocol

MESI

  • Modified
    • Have modified cached data, must write back to memory
  • Exclusive
    • Not modified, I have only copy
  • Shared
    • Not modified, may be cached elsewhere
  • Invalid
    • Cache contents not meaningful

Write-Through Cache

  • Immediately broadcast changes / flush to memory
  • Pros
    • Memory, caches always agree
    • More read hits maybe
  • Cons
    • Bus traffic on all writes
    • Most writes to unshared data -> meaningless broadcasting

Write-Back Caches

  • Accumulate changes in cache
  • Write back when line evicted
    • Need the cache for something else
    • Another processor wants it

MOESI

  • Owned

MOESIF

  • Forward
    • If current cache line owns recent version of variable, forward value to other’s cache line

Back to Spin-Locks

  • Must optimize
    • Bus bandwidth used by spinning threads
    • Release / Acquire latency
    • Acquire latency for idle lock

TAS Lock

  • TAS invalidates cache lines
  • Spinners
    • Miss in cache
    • Go to bus
  • Thread wants to release lock -> delayed behind spinners

TTAS Lock

  • Wait until lock “looks” free
    • Spin on local cache
    • No bus use while lock is busy
  • Problem: when lock is released -> invalidation storm
    • every other threads reread from memory & tries TAS(again invalidating others’ caches)

Exponential Backoff Lock

  • If I fail to get lock
    • Wait random duration before retry
    • Each subsequent failure doubles expected wait
public class Backoff implements Lock {
  public void lock() {
    int delay = MIN_DELAY;
    while (true) {
      while (state.get()) {};
      if (!ock.getAndSet(true))
        return;
      sleep(random() % delay);
      if (delay < MAX_DELAY)
        delay = 2 * delay;
    }
  }
}
  • Pros
    • Easy to implement / beats TTAS lock
  • Cons
    • Must choose parameters carefully
    • Not portable across platforms

Anderson Queue Lock

  • Avoid useless invalidations
    • By keeping a queue of threads
  • Each thread notifies next in queue without bothering the others
    • Reduce cache invalidation
  • Pros
    • Shorter handover than backoff
    • Scalable performance
    • FCFS
  • Cons
    • space complexity O(LN)
    • Many bits share the same cache line -> need to align them
class ALock implements Lock {
  boolean[] flags {true, false, false, ... , false};
  AtomicInteger next = new AtomicInteger(0);
  ThreadLocal<Integer> mySlot;

  public void lock() {
    mySlot = next.getAndIncrement();
    while (!flags[mySlot % N]) {}; // spin while mySlot is false
    flags[mySlot % N] = false;
  }

  public void unlock() {
    flags[(mySlot+1) % N] = true;
  }
}

CLH Queue Lock

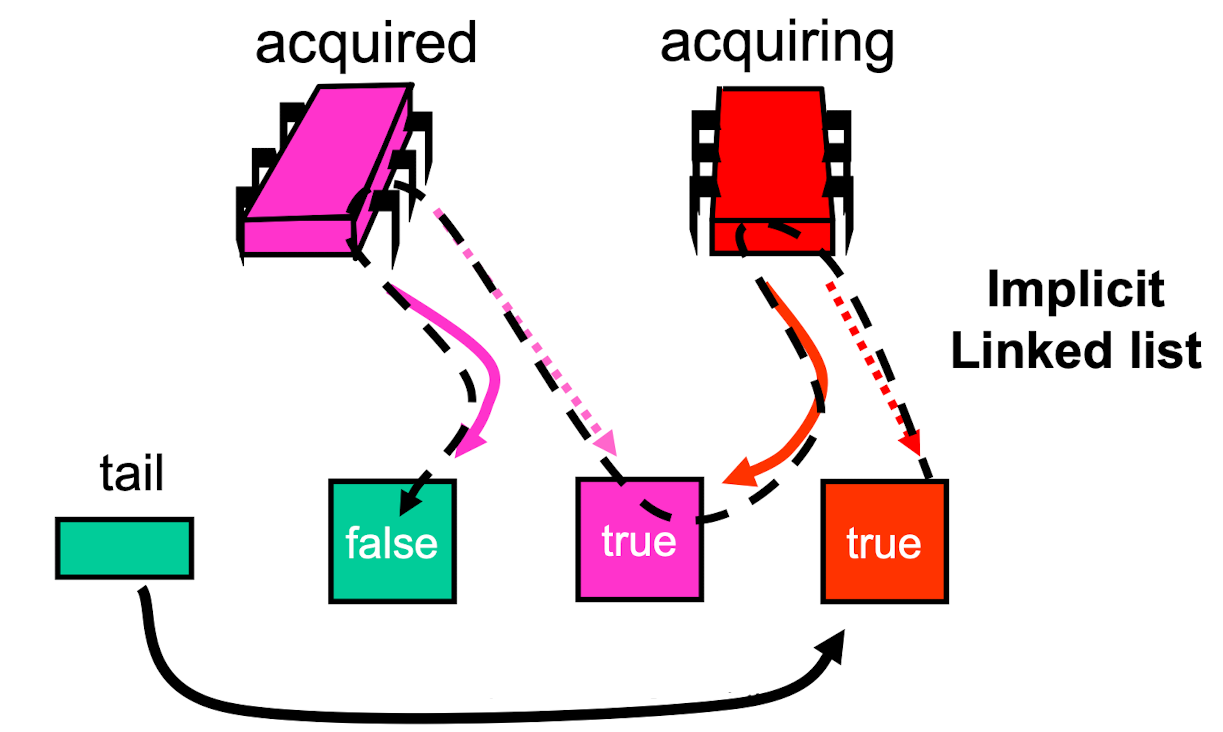
clh lock

class QNode {
  AtomicBoolean locked; // true means not released yet
  public QNode(boolean value) {
    locked = new AtomicBoolean(value);
  }
}

class CLHLock implements Lock {
  AtomicReference<QNode> tail = new QNode(false);
  ThreadLock<QNode> myNode = new QNode(true);

  public void lock() {
    QNode pred = tail.getAndSet(myNode);
    while (pred.locked) ();
  }

  public void unlock() {
    myNode.locked.set(false);
  }
}
  • Pros
    • Small, constant-size overhead per thread
    • FCFS
    • Lock release affects predecessor only
    • Space complexity: O(L+N)
  • Cons
    • Doesn’t work for uncached NUMA architectures (intel)
    • May spin on different region(predecessor’s ) of memory.

MCS Lock

mcs lock

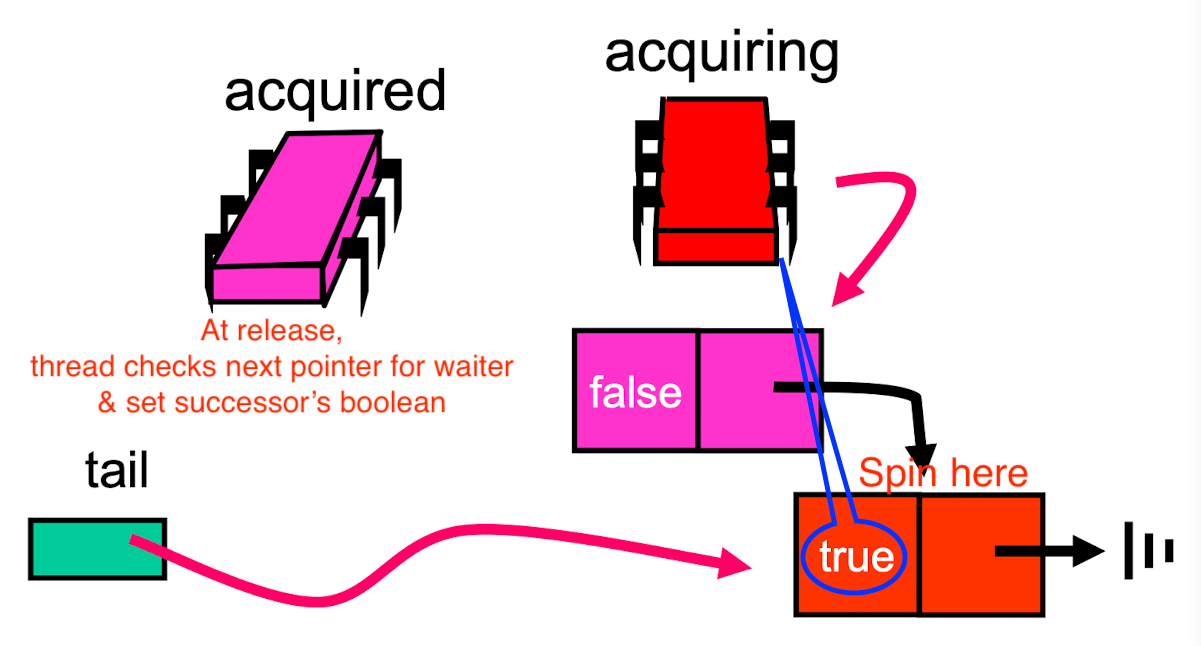
class QNode {
  volatile boolean locked;
  volatile QNode   next;

  public QNode(boolean value) {
    locked = value;
    next = null;
  }
}

class MCSLock implements Lock {
  AtomicReference tail;

  public void lock() {
    QNode qnode = new QNode(false);
    QNode pred = tail.getAndSet(qnode);
    if (pred != null) {
      qnode.locked = true;
      pred.next = qnode;
      while (qnode.locked) {};
    }
  }

  public void unlock() {
    if (qnode.next == null) {
      if (tail.CAS(qnode, null))
        return; // There is no successor
      while (qnode.next == null) {}; // Wait for successor to finish pointer changing job.
    }

    qnode.next.locked = false;
  }
}
  • Pros
    • FCFS
    • Spin on local memory only
    • Small, constant-size overhead

Concurrent Linked List

Coarse-Grained Synchronization

  • Sequential bottleneck
    • Threads “stand in line”
  • Adding more threads does not improve throughput

Fine-Grained Synchronization

  • Split object into independently-synchronized components
    • Instead of using a single lock
    • Methods conflict when they access…
      • The same component
      • At the same time
  • Hand-over-Hand locking

Optimistic Synchronization

  • Search without locking
  • If item is found, lock & check…
    • Validation of locked component
    • If fail, start over -> expensive
  • Validation
    • After acquire two locks, make sure…
      • First item is accessible from the head
      • Second item is successor of first item

Lazy Synchronization

  • Postponed hard work
  • Remove in two steps
    • Logical removal
      • Mark component to be deleted
    • Physical removal
      • Do what needs to be done
  • Validation
    • After acquire two locks, make sure…
      • pred & curr is not marked
      • pred.next == curr

Lock-Free Synchronization

  • Don’t use locks at all
    • Use CAS & TAS… atomic actions
  • Pros
    • No scheduler assumptions/support
  • Cons
    • Complex
    • Sometimes high overhead
  • Combine pointer with valid bit
    • Use CAS to verify pointer & valid bit

Representation Invariant

  • 표현 불변성
  • Correctness
    • Property that always hold
  • Established because
    • True when object is created
    • Truth preserved by each step of each method

Concurrent Queue & Stack

Terminology

  • Bounded
    • Fixed capacity
  • Unbounded
    • Unlimited capacity
  • Blocking
    • Block on attempt to remove from empty structure
    • Block on attempt to add to full bounded structure
  • Non-Blocking
    • Throw exception on such attempts explained above

Bounded, Blocking, Lock-Based Queue

public interface Condition {
  void await();
  boolean await(long time, TimeUnit unit);
  void signal();
  void signalAll();
}

public class BoundedQueue<T> {
  ReentrantLock enqLock = new ReentrantLock();
  ReentrantLock deqLock = new ReentrantLock();
  Condition notFullCondition = enqLock.newCondition();
  Condition notEmptyCondition = deqLock.newCondition();
  int capacity;
  AtomicInteger size;
  Node head;
  Node tail;

  public void enq(T x) {
    boolean mustWakeDequeuers = false;
    enqLock.lock();

    // Queue is full wait for the signal
    while (size.get() == Capacity)
      notFullCondition.await();

    Node e = new Node(x);
    tail.next = e;
    tail = tail.next;
    if (size.getAndIncrement() == 0)
      mustWakeDequeuers = true;
    enqLock.unlock();

    if (mustWakeDequeuers) {
      deqLock.lock();
      notEmptyCondition.signalAll();
      deqLock.unlock();
    }
  }
}
  • enq() & deq() does not share locks
    • But they do share an atomic counter size
    • Bottleneck!

Unbounded, Backoff, Lock-Free Stack

public class LockFreeStack {
  private AtomicReference top = new AtomicReference(null);

 public boolean tryPush(Node node) {
    Node oldTop = top.get();
    node.next = oldTop;
    return (top.compareAndSet(oldTop, node));
  }

  public void push(T value) {
    Node node = new Node(value);
    while (true) {
      if (tryPush(node))
        return;
      else
        backoff.backoff();
    }
  }
}
  • ABA problem might occur without GC
    • Use Stamped Reference

Elimination-Backoff Stack

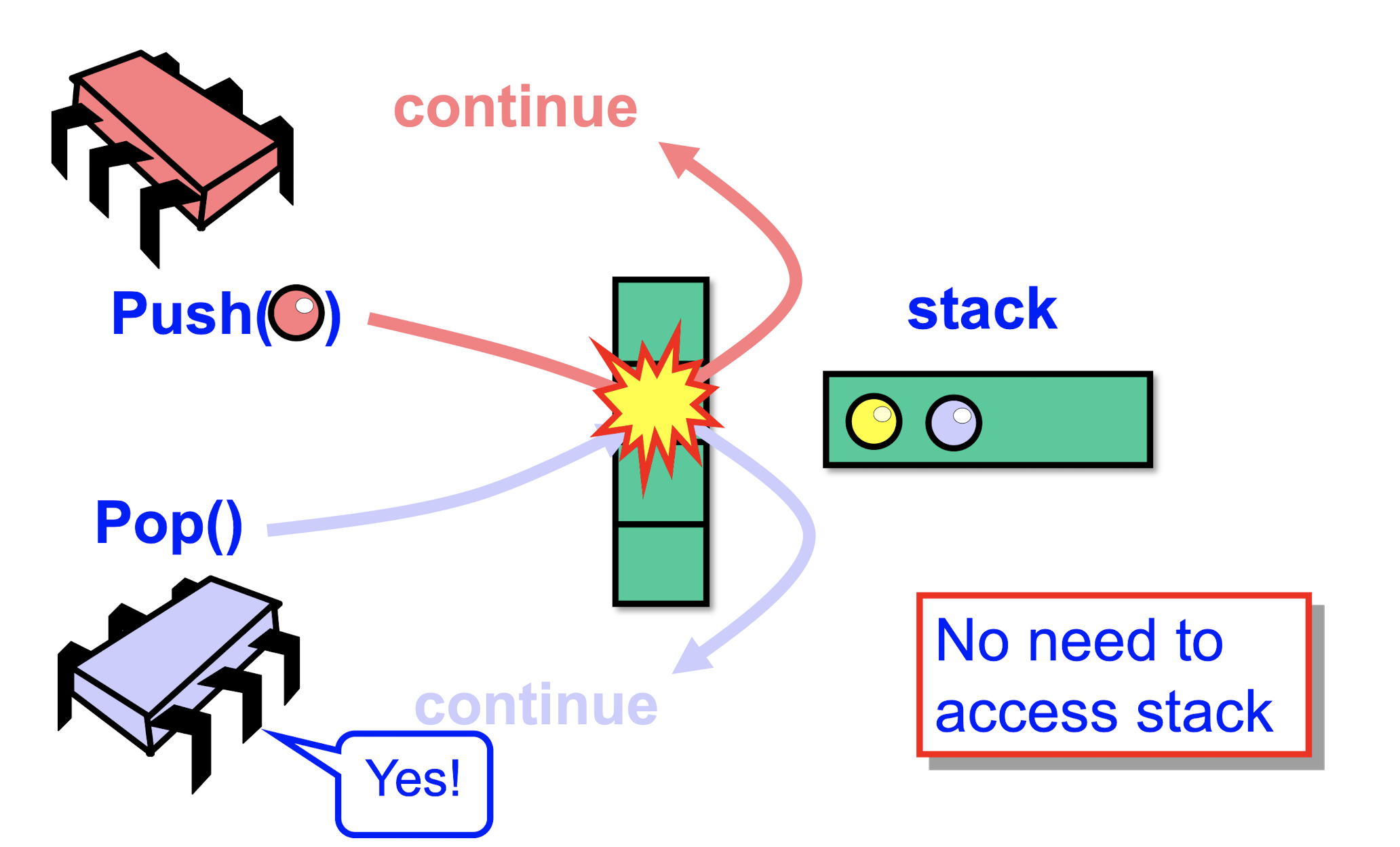
elimination array

  • Use Elimination Array to store temporary values during the function call
  • Access Lock-Free stack,
    • If uncontended, apply operation
    • If contended back off to elimination array
  • If collision occurs, pop element without reaching stack